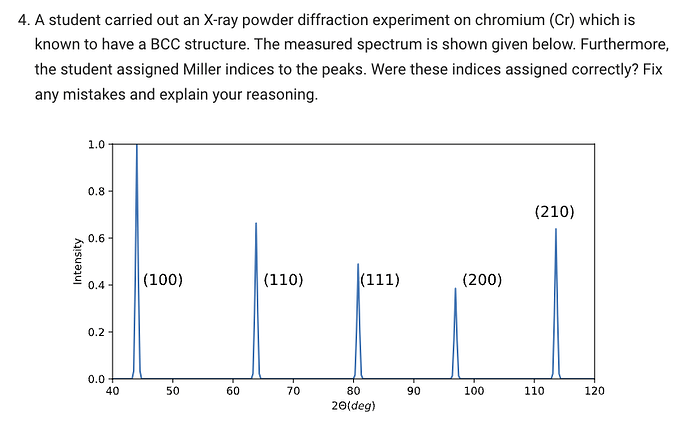
How can you determine which peaks are correct and which aren’t?
In the image you can see peaks (100), (110), (111), (200), (210)
(100): I don’t know why this value is not correct. It is (like other correct answers) a combination of even and odd numbers.
(110): I don’t know why this value is correct.
(111): I can understand why this value is incorrect. Peaks that only contain odd numbers are incorrect, since the structure factor is zero for these values.
(200): Is correct, but I don’t know why.
(210): Correct but I don’t know why.
The answer model says: " 1. Due to the systematic absences of peaks caused by the structure factor, the peaks from lowest to largest angle are: (110), (200), (211), (220), (310).
I think I should use Braggs law and the distance between the Miller planes, but I don’t know how.
I believe this is because we found in question 4.2 that the visible peaks must correspond to Miller indices (hkl) for which h+k+l=even, since combinations of indices such that h+k+l=odd lead to zero intensity. Hope that helps!
From your comments on (100) and (111), it looks like you were also a bit confused with the outcome from the structure factor computed under The Laue condition and structure factor for non-primitive unit cells, where it was found for an FCC that h,k,l must all be even or odd to have a non-zero structure factor S.
- This result of the structure factor was for an FCC lattice, but here in Q4 we have a BCC, so the structure factor is different (as found in 4.2).
- The “h,k,l must all be even or odd” for the FCC doesn’t mean that the Miller indices should be a combination of even and odd values, but it means that h,k and l must either all be even, or all be odd (otherwise the exponents are not all multiples of 2\pi, try it out :))
Anyone please correct me if I’m wrong!
That is exactly correct @lucienne , thanks for your help. @cboonstra please try out the exercise now with these new insights from Lucienne, if it doesn’t work just let us know here. We’ll be happy to help.
Best,
Álvaro
I was wondering if for a question like this it matters how the Miller indices are done? Geometrically I understand (1 1 0) to be different from (0 1 1) but using those numbers here would result in a mathematically equivalent answer. So if this question were to come up in an exam for example, would it matter whether I answered (1 1 0) or (0 1 1) for the first peak?
Additionally, why is (2 2 2) not one of the Miller planes that represents a peak? Is this because its index total (h + k + l = 6) is lower than (3 1 0) (h + k + l = 4) and therefore it is not one of the first five?
Exactly, for determining which ones are gonna be present it doesn’t matter the order of the indices. (110) is gonna be the same as (101). In case you are curious actually the multiplicity of Miller indices that lead to a given peak is one of the factors that determines the intensity.
For your second questions, yes, that’s the logic.