Tight binding DOS different in notes than from book

Site Feedback
1

Hi, looking through the book I found this expression for the DOS in a 1D monoatomic chain on page 84.

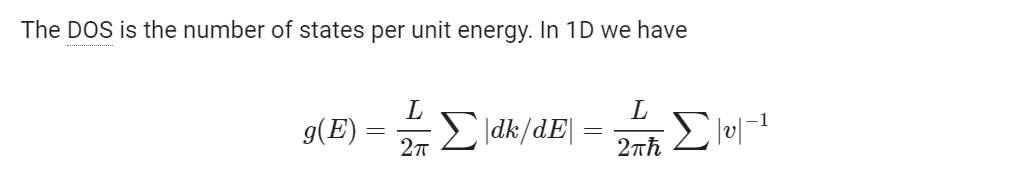
image

//
In the lecture notes we’re given this expression
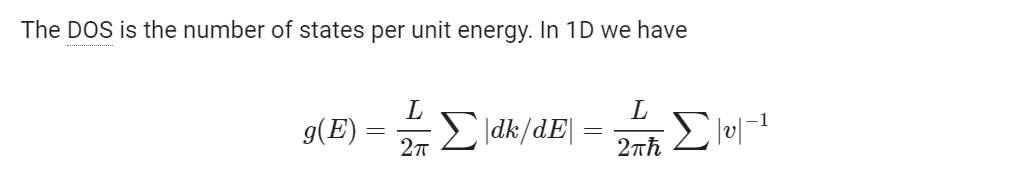
image

is there a factor 2 missing in the lecture notes ?

2

Hi Maia,

Yes, indeed, it seems so!
Here is my example of the explicit derivation for a 1D chain.

g_{1D}(E)=\frac{dN}{dE} = \frac{dN}{dk'} \frac{dk'}{dE} = \frac{d}{dk'} \frac{L}{2\pi} \int_{-k}^{k} dk' \frac{dk'}{dE} = \frac{d}{dk'} \frac{L}{\pi} \int_{0}^{k} |\frac{dk'}{dE}| dk'

and I used Riemann sum to convert the integral into a sum over k in the following way:

g_{1D}(E) = \frac{d}{dk'} \frac{L}{\pi} \int_{0}^{k} |\frac{dk'}{dE}| dk' = \frac{d}{dk'} \frac{L}{\pi} \sum_{k}|\frac{dk}{dE}| dk' = \frac{L}{\pi} \sum_{k}|\frac{dk}{dE}| = \frac{L}{ \pi \hbar} \sum_{k}|v|^{-1}

@Maia, @team, let me know if you agree and I will update the lecture notes :slight_smile:

1 Like
3

Note the statement “The sum goes over all possible values of k and spin which have the same energy.” As such, working out the sum only yields a factor 4: A factor 2 because of spin, and another factor 2 because of the positive and negative k-values. This factor 4 appears in the final expression g(E) = \frac{L}{2\pi}\frac{4}{a}\frac{1}{\sqrt{4t^2 - (E - E_0)^2}}.

1 Like
4

I agree with your work,

I believe the lecture notes have a factor L/2pi instead of L/pi

5

thanks for the reply, I managed to solve the exercises with this in mind

I saw that in the solutions this expression is used
image

does that then mean that this expression
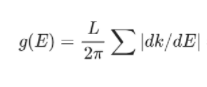
image
does not yet involve the sum in k-space symmetry (2) or spin (2) ?

so once accountint both em those youre left with g(E) = 2L/pi |dk/dE| ?

6

Indeed, the latter expression is still general: you need to sum over all possible values of k and spin (in case of electrons, polarization in case of phonons) which have the same energy. Note that the expression also holds when the dispersion is such that multiple k-values are possible at the same energy. Consider for instance this dispersion for phonons from Ex 1, tight binding:
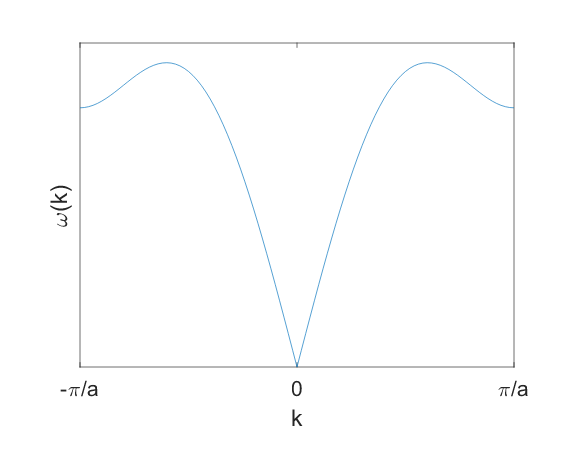
image

To calculate the DOS at a given energy, the sum
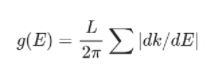
image
runs over all possible values of k at the same energy (for phonons, the sum additionally includes the nr of polarizations). For this particular dispersion, you can see there are multiple k-points corresponding to the same energy for the upper part of the dispersion