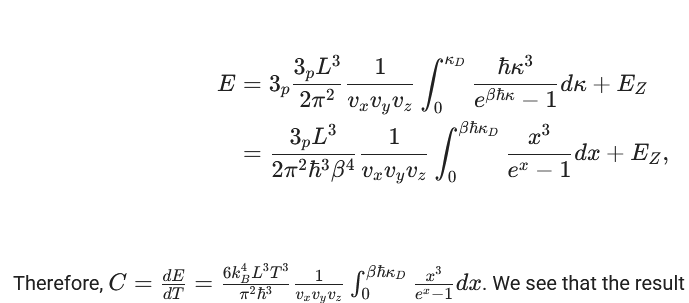Solution to Debye model exercise 4

Physics Q&A
1

In the last exercise of the Debye model, at the very end, this argument is made:

image
image689×303 10.2 KB

but I don’t think the expression for C is valid here, since the integral boundary \beta \hbar k_D depeds on the temperature, and you can’t just ignore that when taking the derivative with respect to T. You’d have to use the Leibniz integral rule. Only in the low temperature limit could you replace the boundary by infinity and take the derivative this way. Could you check?

2

Thanks, well spotted. I have expanded and fixed the solution.

The two options are:

  • Apply the Leibniz rule to differentiate with respect to the integration limit.
  • Differentiate with respect to T before changing the variables in the integrand.

The results are of course the same, but I think the second option leads to a bit more streamlined computation.