
How does the 2pi/|a| form appear in the final expression ?

How does the 2pi/|a| form appear in the final expression ?
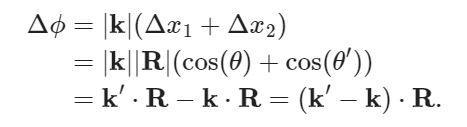
Im wondering how this expression goes from a summation to a subtraction ?
in lecture we were given the following
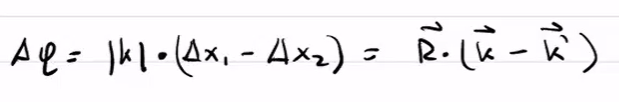
It seems more logical that the phase shift \Delta \phi is a summation
So i’m confused on which one is right
yeah this did me in aswell.
We need to find the path length difference between the two rays. In this case of the picture drawn during the lecture, deltax1 was the extra length traveled by ray 1 and deltax2 that by ray 2, hence the subtraction
ooh I see,
so the example drawing in the lecture and the one in the notes are different then.
So how does this subtraction appear in the lecture notes ?
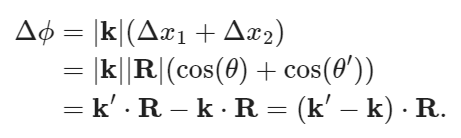
The key idea is to get an expression for the path length difference between the two rays.
One possible point of confusion here is the minus sign. It follows from the inner product \mathbf{k}\cdot \mathbf{R} = |\mathbf{k}||\mathbf{R}|\cos\phi, where \phi=\pi+\theta is the angle between \mathbf{k} and \mathbf{R} when putting the vectors tails to tails
Finally, note that the minus sign makes sense, as the path length difference should vanish when \mathbf{k}=\mathbf{k'}