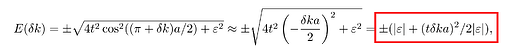I find it hard to see when a certain approximation is appropriate to use. To determine the effective mass at k=0, I first approximated the cosine near k=0. Than I differentiated the whole expression twice and filled in k=0 after which I approximated the square root (using: \epsilon \ll t) to be: 2t+\epsilon^2 /2t, than I again used: \epsilon \ll t to approximate this term to be: 2t (which results in the expression given in the solutions). At what point is the last approximation valid, only when the expresion is linear I guess?
There is no general answer, as it depends on what you are trying to do: suppose you want to derive how a quantity scales with \epsilon, then you should not approximate \epsilon out of the equation. If on the other hand you want to get a good estimate for the quantity at small \epsilon, you can safely approximate it out because the correction by the quadratic term is small
Okay thank you, that makes sense.
@t.vandersar
I have one remaining question about the approximation for k \approx \pi/a.
How should you arrive to the red expression from the square root expression? Both terms in the square root become really small.
this is actually the same as one of your previous questions: Minitest 2 (problem 1, guessing eigenvectors & 2, Taylor expand), and similar problems - #3 by t.vandersar
I see, thank you!