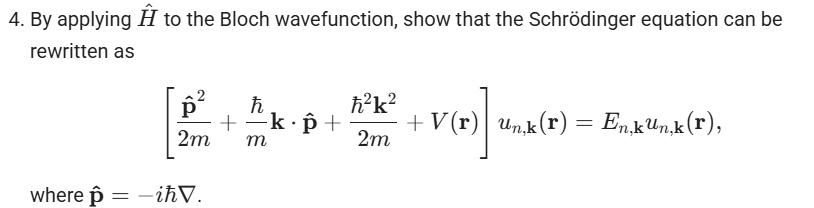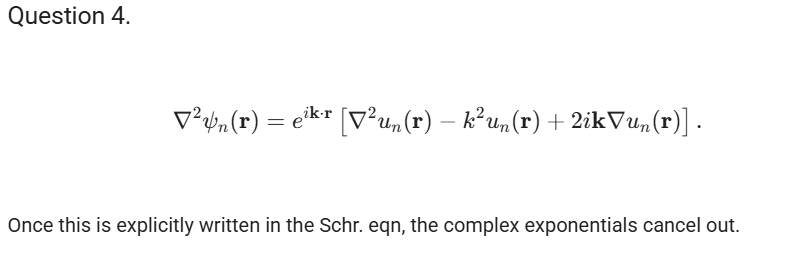Nearly free electron model Q1.4

Physics Q&A
1

I’m working on question 1.4 of the nearly free electron model but I have no clue how to get to the answer of this question.

Here is the question:

image
image814×208 9.17 KB

When looking at the given answer, I’m even more confused:

image
image793×270 7.87 KB

This relation was never talked about in the lecture notes. Can someone please explain how they come to the given answer, thank you!

2

Hi,

Here you should start with the general form of a 3D Hamiltonian, namely:

\hat{H} \;=\; \hat{K} + \hat{V} \;=\; \frac{\hat{\mathbf{p}} \cdot \hat{\mathbf{p}}}{2m} \;+\; \hat{V}(\mathbf{r}) \;=\; -\,\frac{\hbar^{2}}{2m}\,\nabla^{2} \;+\; \hat{V}(\mathbf{r}).

The question then asks you to apply this Hamiltonian to the Bloch wavefunction:

\psi_{n}(\mathbf{r}) \;=\; u_{n}(\mathbf{r})\,e^{i\,\mathbf{k} \cdot \mathbf{r}}

and show that it can be rewritten in the form you have shown above (using the TISE, \hat{H}\psi = E\psi). The answer given in the solutions is just for you to have an intermediate check, to see if you applied the derivatives correctly. This way you still have to do all the work in order to convince yourself that this is what the TISE looks like for the Bloch wavefunction :smiley:.

Does this help?