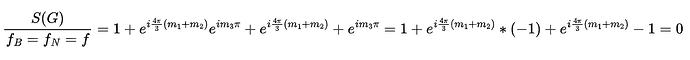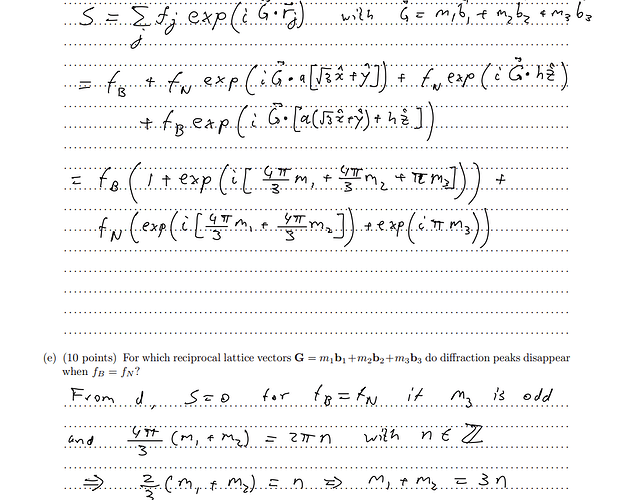Good afternoon,
In the solutions of minitest 3 2019 q1.e, is it says S=0 for m3 is odd and m1+m2 = 3n.
However, is it not true that if m3 is odd, S=0 for all m1 and m2?
In my solution, for m3 = odd the structure factor becomes:
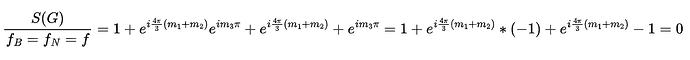
Maybe I made a mistake. Looking forward to your reply.
Kind regards,
Jeroen
Your calculations seem correct, however the problem asks which peaks disappear. It’s been a while since that exam, so let me try to reproduce the solution.
Initially we have:
S = f_B (1 + \exp(4\pi i /3 \times[m_1 + m_2]) \exp(\pi i m_3)) + f_N (\exp(\pi i m_3) + \exp(4\pi i /3 \times [m_1 + m_2]) ).
This solution has missing peaks when \exp(4\pi i /3 \times [m_1 + m_2]) = \exp(\pi i m_3), which is only possible when m_3 = 2n and m_1 + m_2 = 3k.
If f_B = f_N = f, then
S = f(1 + \exp(4\pi i /3 \times [m_1 + m_2]))(1 + \exp(\pi i m_3)),
which vanishes when either m_3 = 2n or m_1 + m_2 = 3k. That means that the peaks that disappear are:
I’ll fix the solutions.
