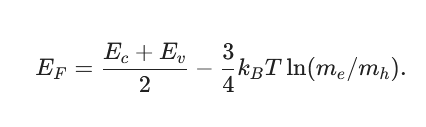In the equation for Fermi Energy from the Basics of Semiconductors lecture, we end up with a term that includes \ln(m_e/m_h):
In the lecture we showed that the effective mass of holes is m_h=-m_e, meaning that our Fermi Energy is imaginary? At least it has an imaginary term -\pi i. I really struggle interpreting that one physically. How does imaginary energy make sense? Or do we just ignore it saying it’s a mathematical artefact? Does this impact other calculations down the road?
There’s an extremely important point we should keep in mind.
We can describe every single particle as either electron or a hole. The properties of that specific hole are in a 1-1 relation with the properties of the same electron. So instead of saying we remove an electron with energy E we can as well say that we add a hole with energy -E. Similarly, the effective mass of an electron and of its absence are opposite. (And of course here let’s remind ourselves that the velocities of an electron and the corresponding hole are the same—both electron and its absence move in the same direction.)
When dealing with semiconductors we always mean electrons from conduction band and holes from the valence band. This is because
Electrons and holes from two different bands are unrelated. Their dispersions are different, and their effective masses are different. Moreover, their masses are both positive. The electron mass in the conduction band is positive since we are looking close to a band minimum. In the valence band the electron mass is negative close to the maximum, but we are considering holes in that band, so their mass is positive too.
Does that answer your question?
Yes it does, thank you very much. I indeed forgot to take into account how mass changes as curvature of the band and the particles energy 
