Hi,
I am struggling with setting up a 4x4 matrix for the Hamiltonian in exercise 3.3 of Band Structures in 2D:
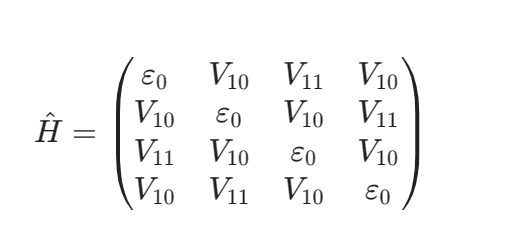
For the point (π/a, 0), I followed this approach:
Now, I am unsure how to proceed for the point (π/a, π/a) based on my previous approach for (π/a, 0). I am confused about the basis used to construct the 4x4 matrix in question 3.3. I also don’t understand why V_10 appears again in the matrix when we are considering the point (π/a, π/a); I expected only V_11 to be present in the matrix.
I think you should look at all the possible combinations The equivalent points of the point \vec{q} = (\pi/a, \pi/a) are the following (already put into some basis):
|1 \rangle = |\pi/a, \pi/a \rangle,
|2 \rangle = |\pi/a, -\pi/a \rangle,
|3 \rangle = |-\pi/a, \pi/a \rangle,
|4 \rangle = |-\pi/a, -\pi/a \rangle
You can see that when calculating: \langle3|V|1\rangle for instance this results in something of the form V_{10}. This can be done for all matrix elements in the chosen basis which should result in the 4\times 4 matrix given in the solutions (Maybe not the exact same result because the exact form of the matrix is basis specific. You should however end up with the same dispersion relation, which isn’t basis specific).
2 Likes
Thanks a lot for your help.
1 Like