The lecture notes give the following equation for the density of states in 1D:
g(E)=\frac{L}{2 \pi} \sum \bigg|\frac{dk}{dE}\bigg|=\frac{L}{2 \pi \hbar} \sum |v|^{-1}
I guess that the definition used to come to this equation is the following:
g(E) = \sum \frac{dN}{dE}= \sum \frac{\partial N}{\partial k} \frac{\partial k}{\partial E}
How does this extend to higher dimensions, and especially how does N change? Furthermore, how must I interput the summation and when is this relevant (and when isn’t it relevant)?
I tried a few things and found the following:
N_{2D} = 2_s\bigg(\frac{L}{2 \pi} \bigg)^2 \int2\pi kdk \Rightarrow \frac{dN_{2D}}{dk} = \frac{d}{dk} \bigg[\int 2_s\bigg(\frac{L}{2 \pi} \bigg)^2(2\pi k) dk \bigg]= 2_s\bigg(\frac{L}{2 \pi} \bigg)^2(2\pi k)
and in 3D:
N_{3D} = 2_s\bigg(\frac{L}{2 \pi} \bigg)^3 \int 4\pi k^2dk \Rightarrow \frac{dN_{3D}}{dk} = \frac{d}{dk} \bigg[\int 2_s\bigg(\frac{L}{2 \pi} \bigg)^3(4 \pi k^2) dk \bigg]= 2_s\bigg(\frac{L}{2 \pi} \bigg)^3(4\pi k^2)
Is this a correct approach?
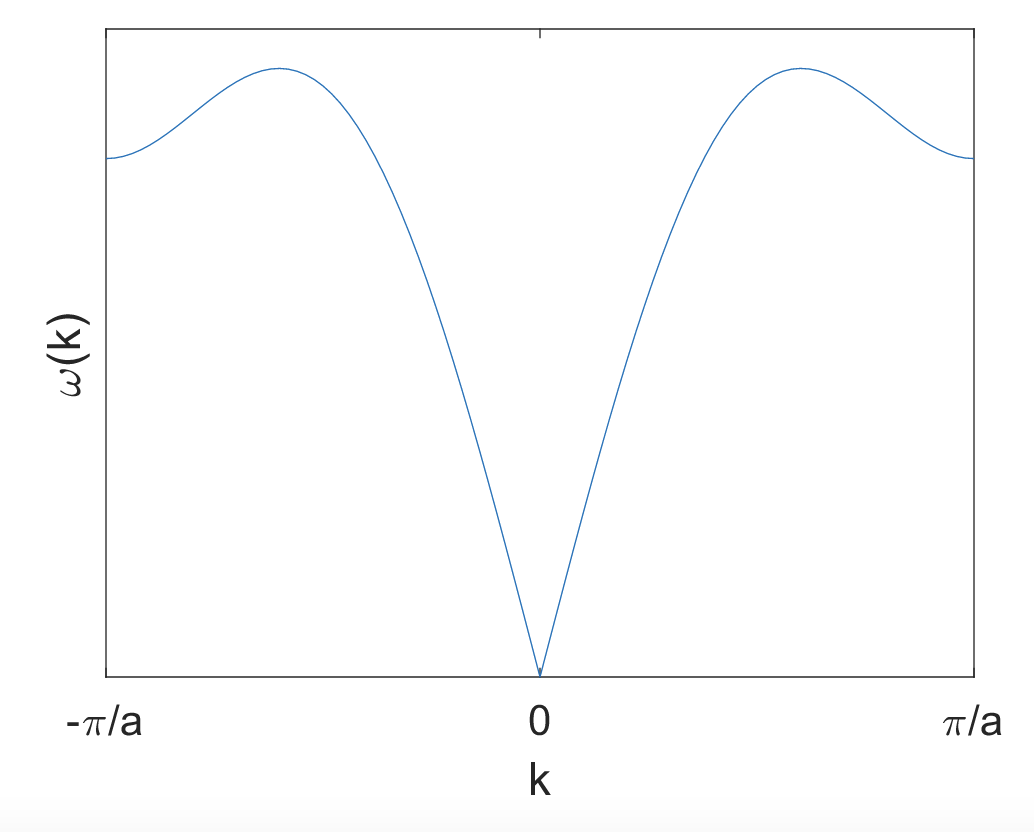
it seems correct to me but I am not sure what you would like to calculate. My suggestion is always to not get lost in the math but instead make a drawing of the dispersion and describe in words how you would calculate the density of states associated with it, and then use that to construct the correct equation. This should also help you understand the sum: it runs over all branches of the dispersion at the same energy. See for instance this dispersion:
and try describing how would you calculate the density of states here.
1 Like