Density of states in higher dimensions

Physics Q&A
1

Hello,

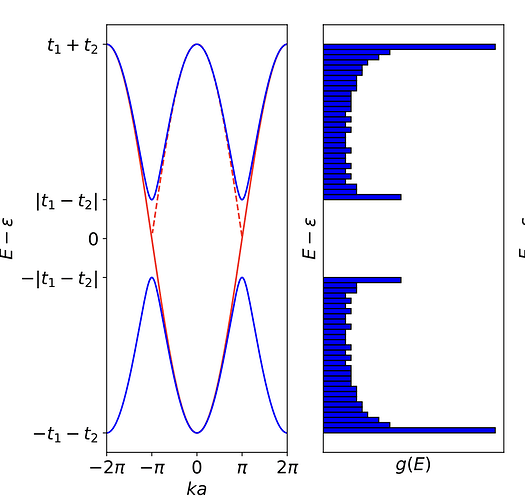
I have a question regarding the density of states in higher dimensions. If we have to graph the density, a useful way was showed in lecture ‘many atoms per unit cell’.

Scherm­afbeelding 2024-05-19 om 22.13.38
Scherm­afbeelding 2024-05-19 om 22.13.38978×930 52.3 KB

However, if I use this method to draw the density of states for for example free electron dispersion, I end up with g(E) ~ 1/sqrt(E). Does this mean that this way of graphing only works for 1D systems? Why is this the case? And is there a way to graph the density of states in this way for higher dimensions? And then how can I determine the relationship between density of states and E for higher dimensions?

Thank you in advance.

2

Indeed, in 1D it is particular straightforward to graphically construct the density of states from the dispersion. Perhaps you saw this already, but in the graph you show above, you can see the 1/sqrt(E) divergence close to the band minima and maxima.

In 2D the procedure is in principle the same: if you make a graph of E vs kx and ky.using e.g. python and then histogram the energy values, you will get the DOS. (just try doing so for a parabolic dispersion to confirm the DOS is constant). However, graphically constructing the DOS for more than 1D on paper is more challenging.